Como hemos comentado en anteriores post, segmentación de clientes es agrupamiento que permite a las empresas comprender sus clientes y orientar la toma de decisiones hacia grupos bien definidos, atendiendo las necesidades especificas en cada uno de ellos. Sin embargo, generalmente en la literatura encontramos aquellos algoritmos de agrupación que utilizan sólo variables numéricas, contrario a esto, en diversas situaciones de la vida real vamos a requerir construir agrupamientos sobre conjuntos de datos que son de tipo mixto (variables numéricas y categóricas). En este post presentamos una metodología que permite realizar agrupamientos cuando se tiene un conjunto de datos de este tipo utilizando la distancia de Gower y el algoritmo PAM (Partitioning Around Medoids).
Distancia de Gower
La distancia de Gower es un coeficiente de similaridad que se basa en diferentes tipos de información de \(n\) variables para medir las semejanzas entre dos individuos. Como la similaridad no es algo que pueda medirse directamente, es necesario transformarla en distancias para así, construir una matriz de similitud. El indice de Gower es un coeficiente que combina diferentes tipos de descriptores y los procesa de acuerdo com su tipo matemático propio. Generalmente, para calcular esa distancia, se utilizan indices binarios así: dos individuos son comparados en una de las variables y se le asigna una puntuación, 0 cuando ellos son considerados como diferentes y 1 cuando tienen algún grado de similitud, para mayor detalle vea [1].
Algoritmo PAM
Partitioning Around Medoids (PAM) fue propuesto por \([2]\) como un método de agrupamiento que mapea desde cualquier métrica de distancia a un número especifico de clúster. El algoritmo se basa en la búsqueda de \(k\) objetos representativos entre los objetos del conjunto de datos, donde, en lugar de utilizar un centroide convencional, PAM utiliza medoides para representar los grupos. Después de encontrar un conjunto de \(k\) objetos representativos, los \(k\) cluster se construyen asignando cada objeto del conjunto de datos al objeto representativo más cercano. A partir de ahí, se determina un nuevo medoide que puede representar mejor al grupo. Todos los elementos de datos restantes se asignan una vez más a los grupos que tienen el medoide más cercano. En cada iteración, los medoides alteran su ubicación. El método minimiza la suma de las diferencias entre cada elemento de datos y su medoide correspondiente. Este ciclo se repite hasta que ningún medoide cambia su ubicación \([2][3][4]\). Para ilustrar esta metodología vamos a utilizar un conjunto de datos publicado en el repositorio de UCI Machine Learning. Este conjunto de datos trata sobre los niveles de obesidad en individuos de México, Perú y Colombia, con base en sus hábitos alimenticios y condición física. En la tabla a continuación mostramos su estructura:
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female | 21 | 1.62 | 64.0 | yes | no | 2 | 3 | Sometimes | no | 2 | no | 0 | 1 | no | Public_Transportation | Normal_Weight |
| Female | 21 | 1.52 | 56.0 | yes | no | 3 | 3 | Sometimes | yes | 3 | yes | 3 | 0 | Sometimes | Public_Transportation | Normal_Weight |
| Male | 23 | 1.80 | 77.0 | yes | no | 2 | 3 | Sometimes | no | 2 | no | 2 | 1 | Frequently | Public_Transportation | Normal_Weight |
| Male | 27 | 1.80 | 87.0 | no | no | 3 | 3 | Sometimes | no | 2 | no | 2 | 0 | Frequently | Walking | Overweight_Level_I |
| Male | 22 | 1.78 | 89.8 | no | no | 2 | 1 | Sometimes | no | 2 | no | 0 | 0 | Sometimes | Public_Transportation | Overweight_Level_II |
| Male | 29 | 1.62 | 53.0 | no | yes | 2 | 3 | Sometimes | no | 2 | no | 0 | 0 | Sometimes | Automobile | Normal_Weight |
La pregunta que inicialmente nos hacemos es cuántos cluster debemos construir? Pues bien, actualmente existen diferentes métodos para evaluar los resultados en un análisis de clúster, por ejemplo densidad, cohesión, separación y radio de los cluster formados. En este post vamos a usar el coeficiente de silueta para evaluar la calidad del agrupamiento obtenido y decidir cuántos agrupamiento realizar.
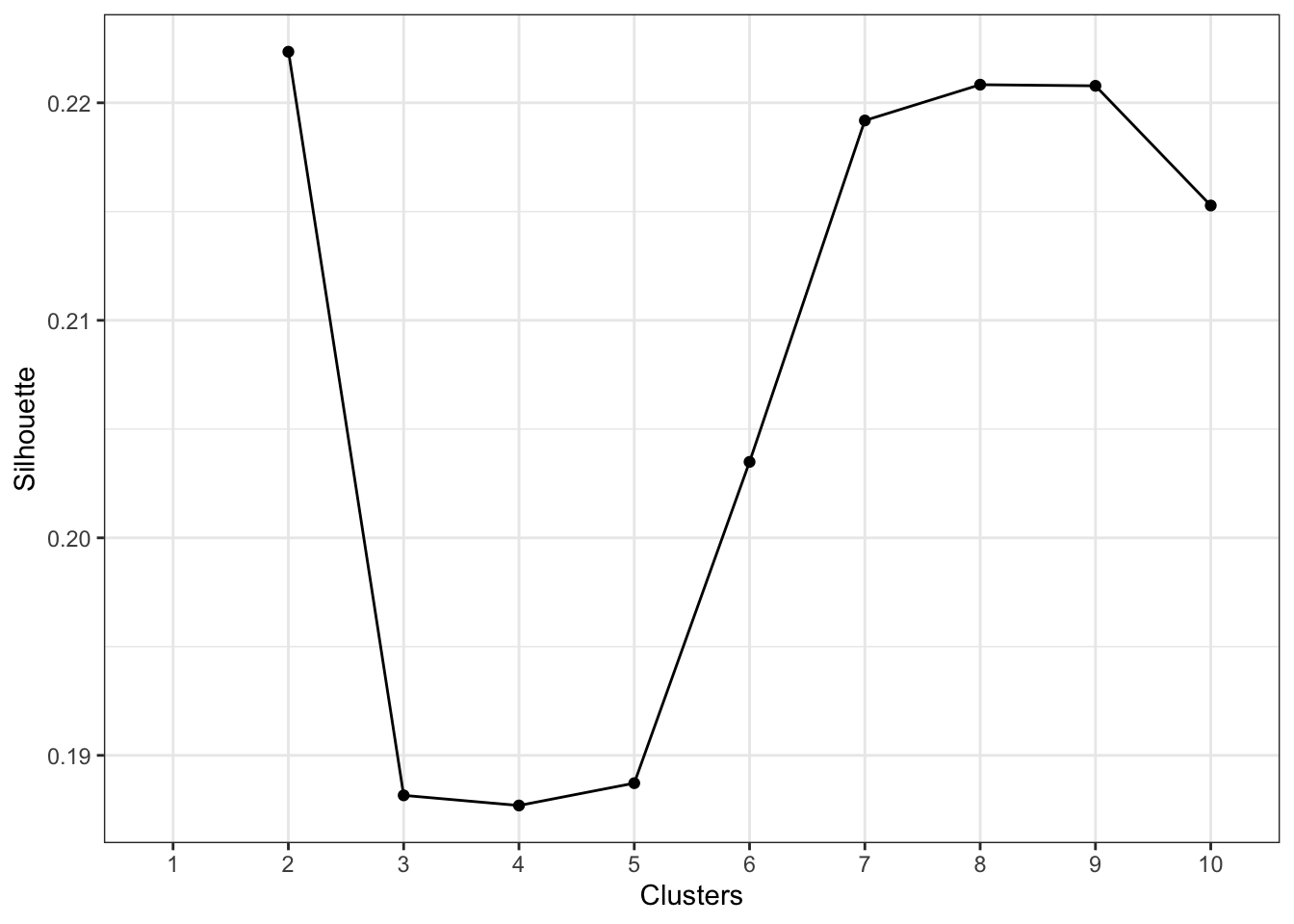
El gráfico del coeficiente de silueta nos sugiere decidir entre 2 y 8 cluster, sin embargo, con fines ilustrativos vamos a construir 4 agrupamientos. En el gráfico a seguir podemos ver una representación de los 4 clúster.

Finalmente podemos hacer un resumen de cada clúster
Clúster 1
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:177 | Min. :14.00 | Min. :1.482 | Min. : 42.30 | yes:490 | yes:469 | Min. :1.000 | Min. :1.000 | Sometimes :467 | yes: 9 | Min. :1.000 | yes: 18 | Min. :0.0000 | Min. :0.00000 | Sometimes : 45 | Public_Transportation:373 | Normal_Weight : 75 | Min. :1 | |
| Male :367 | 1st Qu.:19.00 | 1st Qu.:1.650 | 1st Qu.: 68.71 | no : 54 | no : 75 | 1st Qu.:2.000 | 1st Qu.:1.927 | Sometimes : 0 | no :535 | 1st Qu.:1.876 | no :526 | 1st Qu.:0.3894 | 1st Qu.:0.04627 | Sometimes : 0 | Walking : 15 | Overweight_Level_I : 48 | 1st Qu.:1 | |
| NA | Median :21.93 | Median :1.700 | Median : 82.22 | NA | NA | Median :2.000 | Median :3.000 | Frequently: 58 | NA | Median :2.000 | NA | Median :1.0000 | Median :1.00000 | Frequently: 33 | Automobile :148 | Overweight_Level_II:106 | Median :1 | |
| NA | Mean :23.77 | Mean :1.707 | Mean : 82.22 | NA | NA | Mean :2.241 | Mean :2.583 | Always : 13 | NA | Mean :2.073 | NA | Mean :1.2036 | Mean :0.86699 | Always : 1 | Motorbike : 5 | Obesity_Type_I :224 | Mean :1 | |
| NA | 3rd Qu.:24.50 | 3rd Qu.:1.778 | 3rd Qu.: 95.30 | NA | NA | 3rd Qu.:2.610 | 3rd Qu.:3.000 | no : 6 | NA | 3rd Qu.:2.507 | NA | 3rd Qu.:2.0000 | 3rd Qu.:1.36605 | no :465 | Bike : 3 | Insufficient_Weight: 60 | 3rd Qu.:1 | |
| NA | Max. :55.25 | Max. :1.980 | Max. :125.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.00000 | NA | NA | Obesity_Type_II : 31 | Max. :1 |
Clúster 2
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:606 | Min. :16.00 | Min. :1.480 | Min. : 45.00 | yes:600 | yes:555 | Min. :1.00 | Min. :1.000 | Sometimes :552 | yes: 11 | Min. :1.000 | yes: 19 | Min. :0.0000 | Min. :0.00000 | Sometimes :530 | Public_Transportation:478 | Normal_Weight : 52 | Min. :2 | |
| Male : 0 | 1st Qu.:21.00 | 1st Qu.:1.613 | 1st Qu.: 75.84 | no : 6 | no : 51 | 1st Qu.:2.59 | 1st Qu.:3.000 | Sometimes : 0 | no :595 | 1st Qu.:1.582 | no :587 | 1st Qu.:0.0000 | 1st Qu.:0.09234 | Sometimes : 0 | Walking : 7 | Overweight_Level_I : 90 | 1st Qu.:2 | |
| NA | Median :25.19 | Median :1.650 | Median :104.59 | NA | NA | Median :3.00 | Median :3.000 | Frequently: 34 | NA | Median :2.000 | NA | Median :0.3296 | Median :0.55856 | Frequently: 20 | Automobile :119 | Overweight_Level_II: 57 | Median :2 | |
| NA | Mean :25.43 | Mean :1.660 | Mean : 97.88 | NA | NA | Mean :2.73 | Mean :2.756 | Always : 12 | NA | Mean :2.058 | NA | Mean :0.7038 | Mean :0.56154 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 75 | Mean :2 | |
| NA | 3rd Qu.:26.00 | 3rd Qu.:1.717 | 3rd Qu.:113.43 | NA | NA | 3rd Qu.:3.00 | 3rd Qu.:3.000 | no : 8 | NA | 3rd Qu.:2.619 | NA | 3rd Qu.:1.4140 | 3rd Qu.:0.88974 | no : 56 | Bike : 0 | Insufficient_Weight: 8 | 3rd Qu.:2 | |
| NA | Max. :51.00 | Max. :1.843 | Max. :165.06 | NA | NA | Max. :3.00 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.00000 | NA | NA | Obesity_Type_II : 1 | Max. :2 |
Clúster 3
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female: 0 | Min. :16.00 | Min. :1.600 | Min. : 45.00 | yes:601 | yes:610 | Min. :1.000 | Min. :1.000 | Sometimes :575 | yes: 21 | Min. :1.000 | yes: 17 | Min. :0.0000 | Min. :0.0000 | Sometimes :602 | Public_Transportation:462 | Normal_Weight : 66 | Min. :3 | |
| Male :653 | 1st Qu.:21.01 | 1st Qu.:1.719 | 1st Qu.: 79.00 | no : 52 | no : 43 | 1st Qu.:2.000 | 1st Qu.:2.702 | Sometimes : 0 | no :632 | 1st Qu.:1.833 | no :636 | 1st Qu.:0.5404 | 1st Qu.:0.0000 | Sometimes : 0 | Walking : 19 | Overweight_Level_I :115 | 1st Qu.:3 | |
| NA | Median :24.05 | Median :1.767 | Median : 95.42 | NA | NA | Median :2.154 | Median :3.000 | Frequently: 30 | NA | Median :2.000 | NA | Median :1.0000 | Median :0.3178 | Frequently: 12 | Automobile :167 | Overweight_Level_II:122 | Median :3 | |
| NA | Mean :25.46 | Mean :1.768 | Mean : 95.69 | NA | NA | Mean :2.281 | Mean :2.733 | Always : 16 | NA | Mean :2.060 | NA | Mean :1.0426 | Mean :0.5187 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 52 | Mean :3 | |
| NA | 3rd Qu.:29.88 | 3rd Qu.:1.817 | 3rd Qu.:116.59 | NA | NA | 3rd Qu.:2.741 | 3rd Qu.:3.000 | no : 32 | NA | 3rd Qu.:2.407 | NA | 3rd Qu.:1.5290 | 3rd Qu.:0.9738 | no : 39 | Bike : 3 | Insufficient_Weight: 33 | 3rd Qu.:3 | |
| NA | Max. :56.00 | Max. :1.930 | Max. :173.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.0000 | NA | NA | Obesity_Type_II :264 | Max. :3 |
Clúster 4
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:260 | Min. :16.00 | Min. :1.450 | Min. :39.00 | yes: 35 | yes:232 | Min. :1.000 | Min. :1.000 | Sometimes :171 | yes: 3 | Min. :1.000 | yes: 42 | Min. :0.0000 | Min. :0.0000 | Sometimes :224 | Public_Transportation:267 | Normal_Weight : 94 | Min. :4 | |
| Male : 48 | 1st Qu.:18.29 | 1st Qu.:1.560 | 1st Qu.:45.00 | no :273 | no : 76 | 1st Qu.:2.000 | 1st Qu.:1.891 | Sometimes : 0 | no :305 | 1st Qu.:1.000 | no :266 | 1st Qu.:0.2036 | 1st Qu.:0.0000 | Sometimes : 0 | Walking : 15 | Overweight_Level_I : 37 | 1st Qu.:4 | |
| NA | Median :19.75 | Median :1.620 | Median :50.00 | NA | NA | Median :2.596 | Median :3.000 | Frequently:120 | NA | Median :1.729 | NA | Median :1.0000 | Median :1.0000 | Frequently: 5 | Automobile : 23 | Overweight_Level_II: 5 | Median :4 | |
| NA | Mean :20.66 | Mean :1.633 | Mean :52.77 | NA | NA | Mean :2.416 | Mean :2.629 | Always : 12 | NA | Mean :1.686 | NA | Mean :1.2033 | Mean :0.7732 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 0 | Mean :4 | |
| NA | 3rd Qu.:21.50 | 3rd Qu.:1.700 | 3rd Qu.:58.00 | NA | NA | 3rd Qu.:3.000 | 3rd Qu.:3.000 | no : 5 | NA | 3rd Qu.:2.000 | NA | 3rd Qu.:2.0000 | 3rd Qu.:1.0000 | no : 79 | Bike : 1 | Insufficient_Weight:171 | 3rd Qu.:4 | |
| NA | Max. :61.00 | Max. :1.900 | Max. :93.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.0000 | NA | NA | Obesity_Type_II : 1 | Max. :4 |
Note que esta metodología es sencilla y fácil de aplicar, sin embargo, es importante recordar la importancia de inspeccionar cada clúster construido, tomando una determinación basada en la comprensión de lo que representan los datos, lo que podría representar y la finalidad de cada grupo.
Referencias
[1] Gower J, 1971, A General Coefficient of Similarity and Some of Its Properties, Biometrics, Vol. 27, No. 4, pp. 857-871.
[2] Kaufman L, Rousseeuw P, 1990, Finding groups in data: an introduction to cluster analysis. John Wiley & Sons.
[3] Aruna B, 2014, K-medoids clustering using partitioning around medoids for performing face recognition, International Journal of Soft Computing, Mathematics and Control, Vol. 3, No. 3.
[4] Van der Laan M, Pollard K and Bryan J, 2003, A new partitioning around medoids algorithm, Journal of Statistical Computation and Simulation, Vol. 73, No. 8.
Traducciones
- pt: Segmentação de clientes: análise de cluster usando o algoritmo Partitioning Around Medoids (PAM)
Ver también
- Análisis de datos: Latent Dirichlet Allocation (LDA) Aplicada en Textos Periodísticos
- Segmentación de clientes: un análisis RFM en Knime
- Business Analytics en Knime
- Un estudio al precio de arrendamiento en Medellin por medio un modelo de arbol de regresion
- Google Form: Importando datos en R y publicando resultados en AnalyStats-App