Como comentamos em posts anteriores, segmentação de clientes é uma metodologia de agrupamento que permite às empresas entenderem seus clientes e orientar a tomada de decisões para grupos bem definidos, atendendo as necessidades específicas de cada um deles. No entanto, geralmente encontramos na literatura algoritmos de agrupamento que usam apenas variáveis numéricas, ao passo que, em várias situações da vida real, precisamos agrupar conjuntos de dados que são do tipo misto (variáveis numéricas e categóricas). Neste artigo apresentamos uma metodologia que permite o agrupamento de dados deste tipo, a partir da distância de Gower e do algoritmo PAM (Partitioning Around Medoids).
Distância de Gower
A distância de Gower é um coeficiente de similaridade baseado em diferentes tipos de informações das \(n\) variáveis e que mede as similaridades entre dois indivíduos. Como similaridade não é algo que pode ser medido diretamente, é necessário transformá-la em distâncias para construir uma matriz de similaridade. O índice de Gower é um coeficiente que combina diferentes tipos de descritores e os processa de acordo com seu próprio tipo matemático. Geralmente, para calcular essa distância, índices binários são usados da seguinte forma: dois indivíduos são comparados em uma das variáveis e a pontuação 0 é atribuída quando eles são considerados diferentes e 1 quando eles têm algum grau de similaridade. Para mais detalhes, consulte[1].
Algoritmo PAM
Partitioning Around Medoids (PAM) foi proposto por \([2]\) como um método de agrupamento que associa qualquer medida de distância a um pré-determinado número de grupos. O algoritmo se baseia na busca de \(k\) objetos representativos, dentre os objetos do conjunto de dados, e em vez de usar um centróide convencional para representar os grupos, o PAM usa medoides. Depois de encontrar um conjunto dos \(k\) objetos representativos, os \(k\) clusters são construídos atribuindo cada objeto do conjunto de dados ao objeto representativo mais próximo. A partir daí, é determinado um novo medóide que pode representar melhor o grupo. Todos os elementos do conjunto de dados restantes são atribuídos mais uma vez aos grupos que possuem o medóide mais próximo. A cada iteração, os medoides alteram sua localização. O método minimiza a soma das diferenças entre cada elemento do conjunto de dados e seu medóide correspondente. Este ciclo é repetido até que nenhum medóide mude mais sua localização \([2][3][4]\). Para ilustrar essa metodologia, vamos usar um conjunto de dados publicado no repositório [UCI Machine Learning] (https://archive.ics.uci.edu/ml/machine-learning-databases/00544/). Este é um conjunto de dados sobre os níveis de obesidade em indivíduos do México, Peru e Colômbia, com base em seus hábitos alimentares e condição física. Na tabela a seguir mostramos sua estrutura:
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female | 21 | 1.62 | 64.0 | yes | no | 2 | 3 | Sometimes | no | 2 | no | 0 | 1 | no | Public_Transportation | Normal_Weight |
| Female | 21 | 1.52 | 56.0 | yes | no | 3 | 3 | Sometimes | yes | 3 | yes | 3 | 0 | Sometimes | Public_Transportation | Normal_Weight |
| Male | 23 | 1.80 | 77.0 | yes | no | 2 | 3 | Sometimes | no | 2 | no | 2 | 1 | Frequently | Public_Transportation | Normal_Weight |
| Male | 27 | 1.80 | 87.0 | no | no | 3 | 3 | Sometimes | no | 2 | no | 2 | 0 | Frequently | Walking | Overweight_Level_I |
| Male | 22 | 1.78 | 89.8 | no | no | 2 | 1 | Sometimes | no | 2 | no | 0 | 0 | Sometimes | Public_Transportation | Overweight_Level_II |
| Male | 29 | 1.62 | 53.0 | no | yes | 2 | 3 | Sometimes | no | 2 | no | 0 | 0 | Sometimes | Automobile | Normal_Weight |
A pergunta que inicialmente fazemos é quantos clusters devemos construir? Bem, atualmente existem diferentes métodos para avaliar os resultados em uma análise de cluster, como por exemplo densidade, coesão, separação e raio dos clusters formados. Neste post vamos usar o coeficiente de silhueta para avaliar a qualidade do agrupamento obtido e decidir quantos agrupamentos realizar.
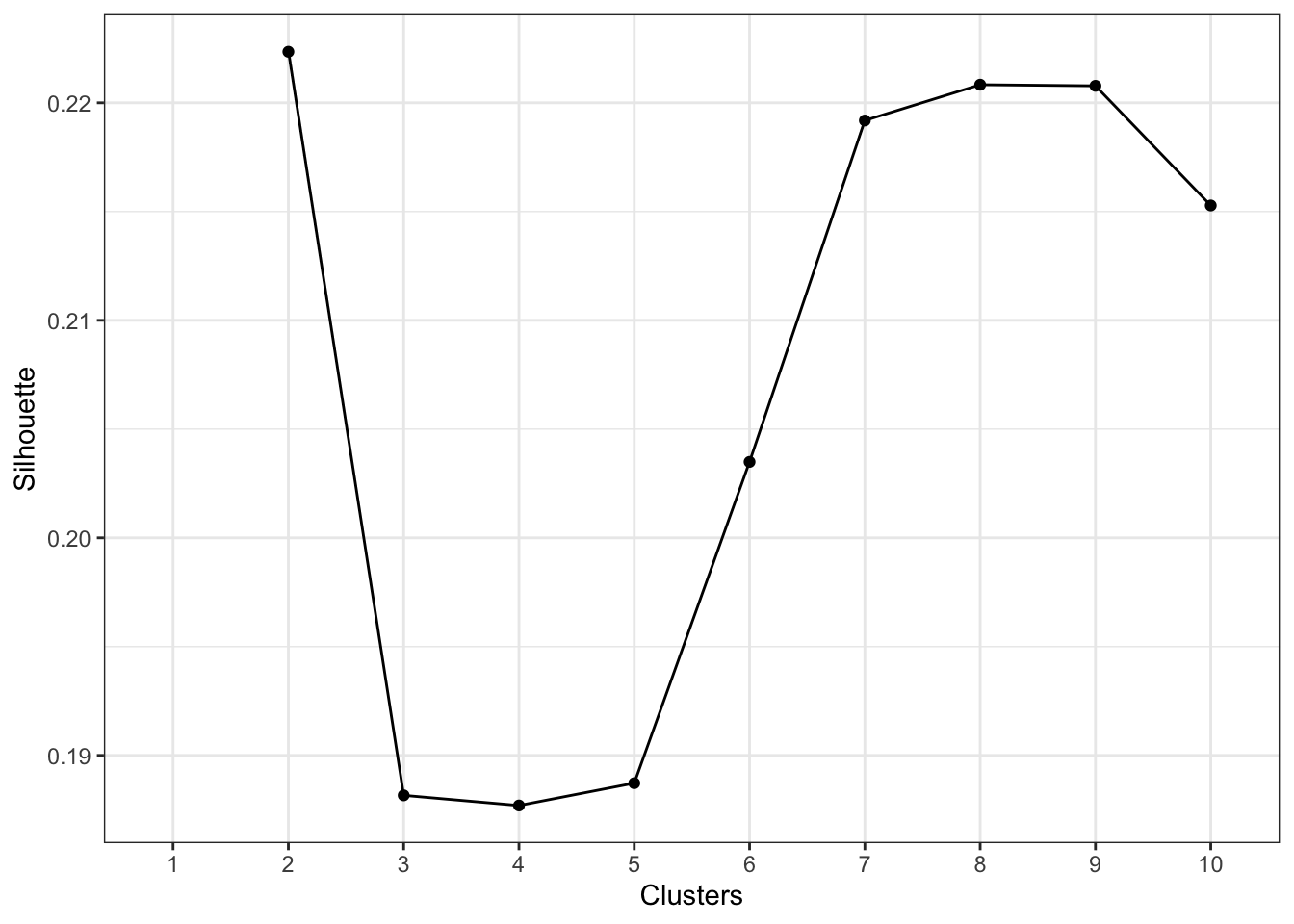
O gráfico do coeficiente de silhueta sugere que devemos decidir entre 2 e 8 clusters, porém, para fins ilustrativos, vamos construir 4 clusters. No gráfico abaixo podemos ver uma representação deles.
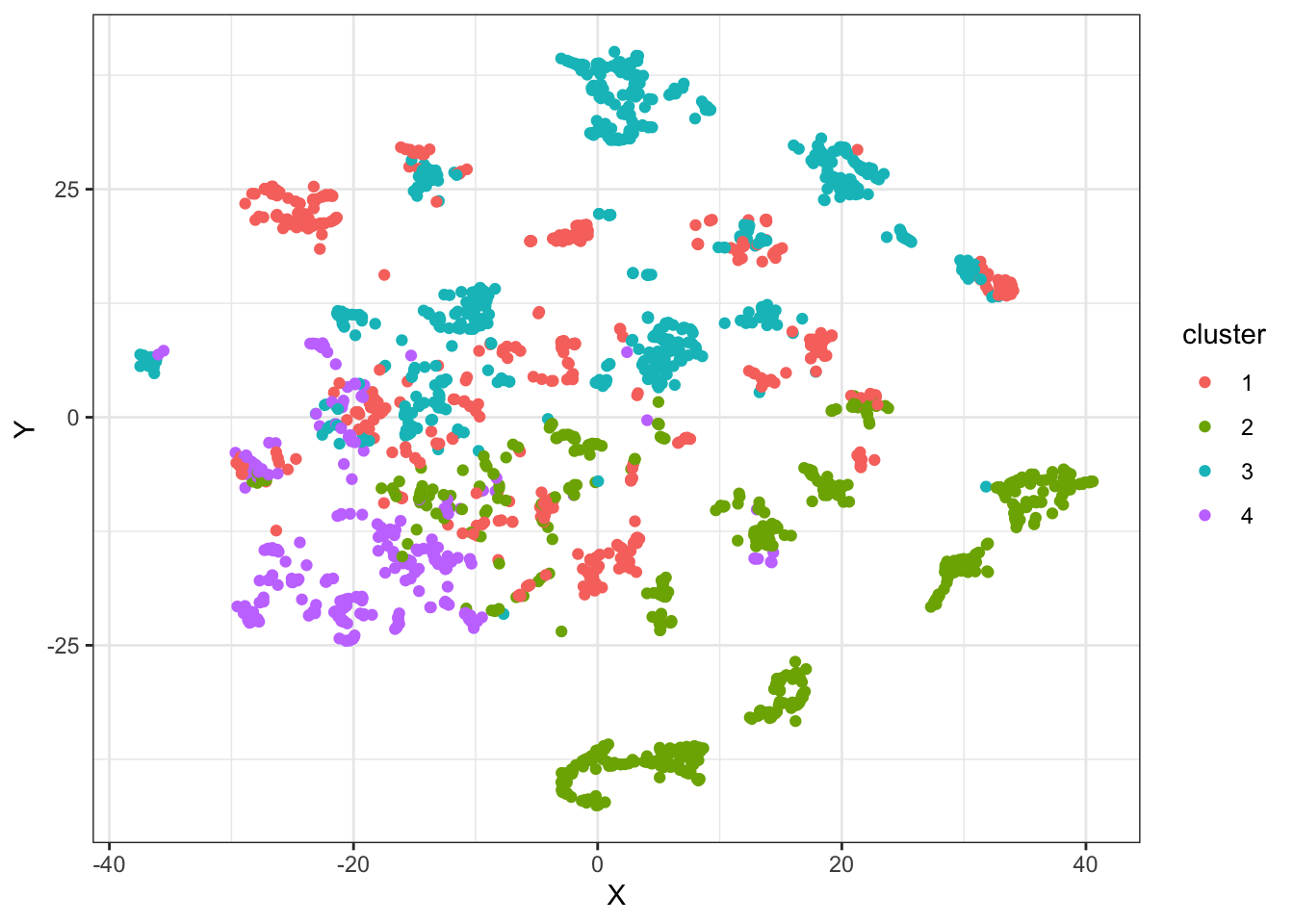
Finalmente podemos fazer um resumo de cada cluster
Cluster 1
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:177 | Min. :14.00 | Min. :1.482 | Min. : 42.30 | yes:490 | yes:469 | Min. :1.000 | Min. :1.000 | Sometimes :467 | yes: 9 | Min. :1.000 | yes: 18 | Min. :0.0000 | Min. :0.00000 | Sometimes : 45 | Public_Transportation:373 | Normal_Weight : 75 | Min. :1 | |
| Male :367 | 1st Qu.:19.00 | 1st Qu.:1.650 | 1st Qu.: 68.71 | no : 54 | no : 75 | 1st Qu.:2.000 | 1st Qu.:1.927 | Sometimes : 0 | no :535 | 1st Qu.:1.876 | no :526 | 1st Qu.:0.3894 | 1st Qu.:0.04627 | Sometimes : 0 | Walking : 15 | Overweight_Level_I : 48 | 1st Qu.:1 | |
| NA | Median :21.93 | Median :1.700 | Median : 82.22 | NA | NA | Median :2.000 | Median :3.000 | Frequently: 58 | NA | Median :2.000 | NA | Median :1.0000 | Median :1.00000 | Frequently: 33 | Automobile :148 | Overweight_Level_II:106 | Median :1 | |
| NA | Mean :23.77 | Mean :1.707 | Mean : 82.22 | NA | NA | Mean :2.241 | Mean :2.583 | Always : 13 | NA | Mean :2.073 | NA | Mean :1.2036 | Mean :0.86699 | Always : 1 | Motorbike : 5 | Obesity_Type_I :224 | Mean :1 | |
| NA | 3rd Qu.:24.50 | 3rd Qu.:1.778 | 3rd Qu.: 95.30 | NA | NA | 3rd Qu.:2.610 | 3rd Qu.:3.000 | no : 6 | NA | 3rd Qu.:2.507 | NA | 3rd Qu.:2.0000 | 3rd Qu.:1.36605 | no :465 | Bike : 3 | Insufficient_Weight: 60 | 3rd Qu.:1 | |
| NA | Max. :55.25 | Max. :1.980 | Max. :125.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.00000 | NA | NA | Obesity_Type_II : 31 | Max. :1 |
Cluster 2
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:606 | Min. :16.00 | Min. :1.480 | Min. : 45.00 | yes:600 | yes:555 | Min. :1.00 | Min. :1.000 | Sometimes :552 | yes: 11 | Min. :1.000 | yes: 19 | Min. :0.0000 | Min. :0.00000 | Sometimes :530 | Public_Transportation:478 | Normal_Weight : 52 | Min. :2 | |
| Male : 0 | 1st Qu.:21.00 | 1st Qu.:1.613 | 1st Qu.: 75.84 | no : 6 | no : 51 | 1st Qu.:2.59 | 1st Qu.:3.000 | Sometimes : 0 | no :595 | 1st Qu.:1.582 | no :587 | 1st Qu.:0.0000 | 1st Qu.:0.09234 | Sometimes : 0 | Walking : 7 | Overweight_Level_I : 90 | 1st Qu.:2 | |
| NA | Median :25.19 | Median :1.650 | Median :104.59 | NA | NA | Median :3.00 | Median :3.000 | Frequently: 34 | NA | Median :2.000 | NA | Median :0.3296 | Median :0.55856 | Frequently: 20 | Automobile :119 | Overweight_Level_II: 57 | Median :2 | |
| NA | Mean :25.43 | Mean :1.660 | Mean : 97.88 | NA | NA | Mean :2.73 | Mean :2.756 | Always : 12 | NA | Mean :2.058 | NA | Mean :0.7038 | Mean :0.56154 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 75 | Mean :2 | |
| NA | 3rd Qu.:26.00 | 3rd Qu.:1.717 | 3rd Qu.:113.43 | NA | NA | 3rd Qu.:3.00 | 3rd Qu.:3.000 | no : 8 | NA | 3rd Qu.:2.619 | NA | 3rd Qu.:1.4140 | 3rd Qu.:0.88974 | no : 56 | Bike : 0 | Insufficient_Weight: 8 | 3rd Qu.:2 | |
| NA | Max. :51.00 | Max. :1.843 | Max. :165.06 | NA | NA | Max. :3.00 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.00000 | NA | NA | Obesity_Type_II : 1 | Max. :2 |
Cluster 3
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female: 0 | Min. :16.00 | Min. :1.600 | Min. : 45.00 | yes:601 | yes:610 | Min. :1.000 | Min. :1.000 | Sometimes :575 | yes: 21 | Min. :1.000 | yes: 17 | Min. :0.0000 | Min. :0.0000 | Sometimes :602 | Public_Transportation:462 | Normal_Weight : 66 | Min. :3 | |
| Male :653 | 1st Qu.:21.01 | 1st Qu.:1.719 | 1st Qu.: 79.00 | no : 52 | no : 43 | 1st Qu.:2.000 | 1st Qu.:2.702 | Sometimes : 0 | no :632 | 1st Qu.:1.833 | no :636 | 1st Qu.:0.5404 | 1st Qu.:0.0000 | Sometimes : 0 | Walking : 19 | Overweight_Level_I :115 | 1st Qu.:3 | |
| NA | Median :24.05 | Median :1.767 | Median : 95.42 | NA | NA | Median :2.154 | Median :3.000 | Frequently: 30 | NA | Median :2.000 | NA | Median :1.0000 | Median :0.3178 | Frequently: 12 | Automobile :167 | Overweight_Level_II:122 | Median :3 | |
| NA | Mean :25.46 | Mean :1.768 | Mean : 95.69 | NA | NA | Mean :2.281 | Mean :2.733 | Always : 16 | NA | Mean :2.060 | NA | Mean :1.0426 | Mean :0.5187 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 52 | Mean :3 | |
| NA | 3rd Qu.:29.88 | 3rd Qu.:1.817 | 3rd Qu.:116.59 | NA | NA | 3rd Qu.:2.741 | 3rd Qu.:3.000 | no : 32 | NA | 3rd Qu.:2.407 | NA | 3rd Qu.:1.5290 | 3rd Qu.:0.9738 | no : 39 | Bike : 3 | Insufficient_Weight: 33 | 3rd Qu.:3 | |
| NA | Max. :56.00 | Max. :1.930 | Max. :173.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.0000 | NA | NA | Obesity_Type_II :264 | Max. :3 |
Cluster 4
| Gender | Age | Height | Weight | family_history_with_overweight | FAVC | FCVC | NCP | CAEC | SMOKE | CH2O | SCC | FAF | TUE | CALC | MTRANS | NObeyesdad | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Female:260 | Min. :16.00 | Min. :1.450 | Min. :39.00 | yes: 35 | yes:232 | Min. :1.000 | Min. :1.000 | Sometimes :171 | yes: 3 | Min. :1.000 | yes: 42 | Min. :0.0000 | Min. :0.0000 | Sometimes :224 | Public_Transportation:267 | Normal_Weight : 94 | Min. :4 | |
| Male : 48 | 1st Qu.:18.29 | 1st Qu.:1.560 | 1st Qu.:45.00 | no :273 | no : 76 | 1st Qu.:2.000 | 1st Qu.:1.891 | Sometimes : 0 | no :305 | 1st Qu.:1.000 | no :266 | 1st Qu.:0.2036 | 1st Qu.:0.0000 | Sometimes : 0 | Walking : 15 | Overweight_Level_I : 37 | 1st Qu.:4 | |
| NA | Median :19.75 | Median :1.620 | Median :50.00 | NA | NA | Median :2.596 | Median :3.000 | Frequently:120 | NA | Median :1.729 | NA | Median :1.0000 | Median :1.0000 | Frequently: 5 | Automobile : 23 | Overweight_Level_II: 5 | Median :4 | |
| NA | Mean :20.66 | Mean :1.633 | Mean :52.77 | NA | NA | Mean :2.416 | Mean :2.629 | Always : 12 | NA | Mean :1.686 | NA | Mean :1.2033 | Mean :0.7732 | Always : 0 | Motorbike : 2 | Obesity_Type_I : 0 | Mean :4 | |
| NA | 3rd Qu.:21.50 | 3rd Qu.:1.700 | 3rd Qu.:58.00 | NA | NA | 3rd Qu.:3.000 | 3rd Qu.:3.000 | no : 5 | NA | 3rd Qu.:2.000 | NA | 3rd Qu.:2.0000 | 3rd Qu.:1.0000 | no : 79 | Bike : 1 | Insufficient_Weight:171 | 3rd Qu.:4 | |
| NA | Max. :61.00 | Max. :1.900 | Max. :93.00 | NA | NA | Max. :3.000 | Max. :4.000 | NA | NA | Max. :3.000 | NA | Max. :3.0000 | Max. :2.0000 | NA | NA | Obesity_Type_II : 1 | Max. :4 |
Note que esta metodologia é simples e fácil de se aplicar, porém é válido ressaltar a importância de se inspecionar cada cluster construído, verificando se o agrupamento é coerente com o contexto dos dados, se variáveis importantes estão tendo efeito, de fato, na construção dos agrupamentos, e se é possível distinguir e descrever o que cada grupo representa.
Referências
[1] Gower J, 1971, A General Coefficient of Similarity and Some of Its Properties, Biometrics, Vol. 27, No. 4, pp. 857-871.
[2] Kaufman L, Rousseeuw P, 1990, Finding groups in data: an introduction to cluster analysis. John Wiley & Sons.
[3] Aruna B, 2014, K-medoids clustering using partitioning around medoids for performing face recognition, International Journal of Soft Computing, Mathematics and Control, Vol. 3, No. 3.
[4] Van der Laan M, Pollard K and Bryan J, 2003, A new partitioning around medoids algorithm, Journal of Statistical Computation and Simulation, Vol. 73, No. 8.
Tradução
Veia Também
- Segmentação de clientes: uma análise RFM em Knime
- Análise de dados: Latent Dirichlet Allocation (LDA) Aplicada em Textos Jornalistícos
- Business Analytics no Knime
- Um estudo do preço de aluguel em Medellín por meio de um modelo de árvore de regressão
- Google Form: Importando dados em R e publicando resultados em AnalyStats-App