Os testes A/B podem ser vistos como experimentos controlados que suportam a tomada de decisão baseada em dados. Esses tipos de experimentos geralmente são usados para medir o impacto das alterações feitas e comparar diferentes alternativas em campanhas de marketing, produtos de software ou sites. Hoje, grandes empresas de tecnologia usam testes A/B para apoiar a tomada de decisões, por exemplo, Facebook [3], Google [4] e Microsoft [5].
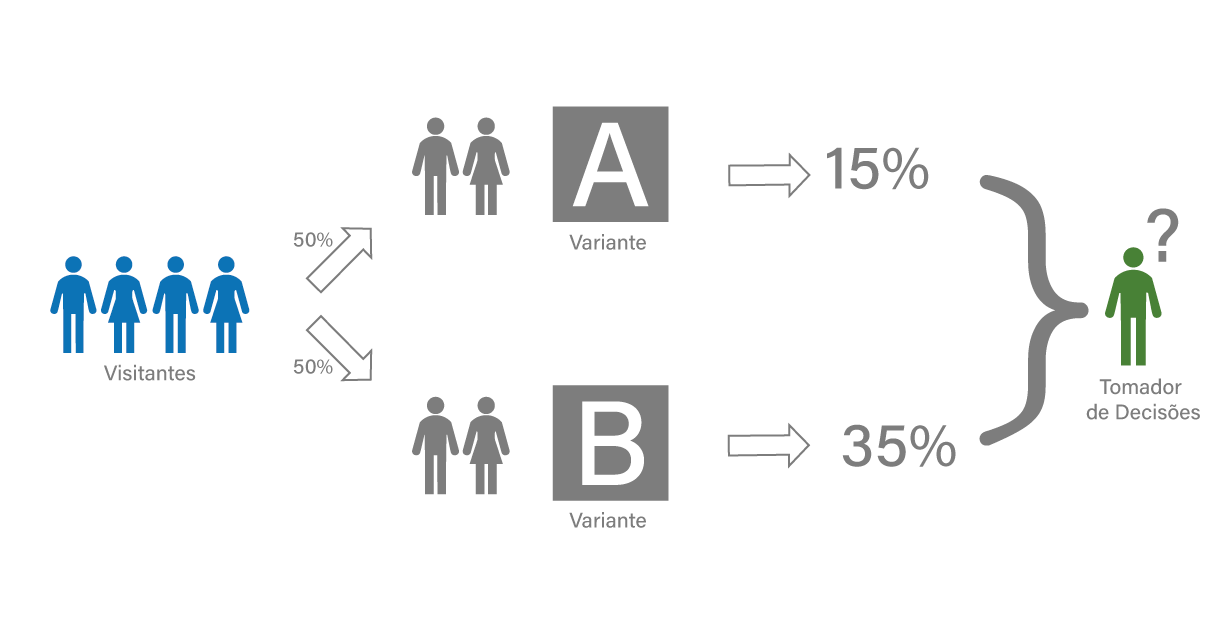
Como mostrado na figura anterior, a ideia de um teste A/B é comparar as taxas de sucesso de cada variante executada (na imagem, variantes A e B). Para comparar essas proporções, geralmente são utilizados os conhecidos t-test e z-test, que resumem o resultado do teste com um valor-p, rejeitando a hipótese de igualdade entre as proporções quando o valor-p é menor que um nível de significado prefixado, geralmente 5%. No entanto, esses tipos de metodologias baseadas no valor-p (ou teste de significância) têm sido amplamente criticados sob diferentes pontos de vista [6][7]. Uma das críticas mais frequentes é conhecida como p-hacking, em que o experimento é interrompido no momento em que o valor-p é menor que o nível de significância predeterminado, favorecendo alguma das variantes.
Por outro lado, as metodologias bayesianas estão ganhando cada vez mais aceitação devido à sua fácil interpretação e implementação. Embora receba algumas críticas por sua sensibilidade na seleção da distribuição a priori, atualmente existem várias maneiras de obter as prioris apropriadas para cada situação, como discutido em [2] . Neste post, apresentamos a metodologia desenvolvida em [1] como uma solução ótima para combater o p-hacking e as várias críticas interpretativas herdadas ao usar o valor-p como uma medida de decisão.
Suponha que queremos entender se uma empresa precisa implementar um novo site ou simplesmente manter um já existente. Para isso, dividimos o número de visitantes em dois grupos A e B. O grupo A representa os usuários que visualizam o novo site e o grupo B representa os usuários que visitam o existente. Para comparar os dois sites, vamos usar a taxa de conversão em cada grupo, isto é, o número de visitantes que concluem o objetivo desejado. Portanto, permita que \(X_ {A}\) represente o número de conversões no grupo A e que \(X_ {B}\) represente o número de conversões no grupo B. Observe que \(X_ {A}\) e \(X_ {B}\) seguem uma distribuição Binomial, ou seja, \(X_ {A}\sim Bin(n_{A},\theta_{A})\) e \(X_ {B}\sim Bin(n_{B},\theta_ {B})\), em que \(n_{(.)}\) representa o número de usuários de cada grupo e \(\theta_{(.)}\) representa a probabilidade de conversão no respectivo grupo.
Modelo estatístico
Para testar se as taxas são estatisticamente iguais, definamos as seguintes hipóteses:
\[\begin{equation}\label{Homogeneity_Bin} \begin{aligned} H_{0}:&\, \theta_{A}=\theta_{B}\\ H_{1}:&\, \theta_{A} \neq \theta_{B}. \end{aligned} \end{equation}\]Pela perspectiva Bayesiana, a hipótese é testada utilizando o fator de Bayes, definido como:
\[ Bf(x)=\frac{f_{H_{0}(x)}}{f_{H_{1}(x)}}=\frac{\displaystyle \int_{\Theta} L(\theta\,|\,x)\pi(\theta\,|\,\theta\in H_{0})\,dP_{H_{0}}(\theta)}{\displaystyle \int_{\Theta} L(\theta\,|\,x)\pi(\theta\,|\,\theta\in H_{1})\,dP_{H_{1}}(\theta)}. \]Para facilitar a notação, indicaremos os visitantes do grupo A como população 1 e os do grupo B como população 2. Assim, temos que \(L(\pmb{\theta}\,|\,\pmb{x})\) é conhecido como a função de verossimilhança e que, no nosso caso, é descrita por:
\[\begin{equation} L(\theta \,|\,x) =\prod_{i=1}^{2} {{n_{i}}\choose{x_{i}}}\theta_{i}^{x_{i}}(1-\theta_{i})^{n_{i}-x_{i}} I(\theta_{i}\in (0,1)). \end{equation}\]Também no paradigma Bayesiano, supõe-se que \(\theta_{A}\) e \(\theta_{B}\) tem distribuição de probabilidade, que neste caso é uma distribuição Beta para cada parâmetro, ou seja:
\[\begin{equation} \pi(\theta_{i})=\frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})}\theta_{i}^{a_{i}-1}(1-\theta_{i})^{b_{i}-1}I(\theta_{i}\in (0,1)),\qquad i=1,2. \end{equation}\]Com essas definições, podemos calcular a distribuição preditiva da hipótese nula como:
\[\begin{equation} \begin{aligned} f_{\scriptscriptstyle H_{0}}(x)=&\displaystyle \int_{\Theta} L(\theta\,|\,x)\pi(\theta\,|\,\theta\in H_{0})\,dP_{H_{0}}(\theta)\\[6pt] =&\frac{\prod_{i=1}^{2}{{n_{i}}\choose{x_{i}}}\Gamma(D)\Gamma(C)\Gamma\left(\sum_{i=1}^{2}(a_{i}+b_{i})-2\right)}{\Gamma(D+C)\Gamma\left(\sum_{i=1}^{2}a_{i}-1\right)\Gamma\left(\sum_{i=1}^{2}b_{i}-1\right)}, \end{aligned} \end{equation}\]em que \(\textstyle D=\sum_{i=1}^{2}(a_{i}+x_{i})-1\), \(C=\sum_{i=1}^{2}(n_{i} + b_{i}-x_{i})-1\). Da mesma forma, a distribuição preditiva na hipótese alternativa é dada por:
\[\begin{equation} \begin{aligned} f_{\scriptscriptstyle H_{1}}(x)=&\displaystyle \int_{\Theta} L(\theta\,|\,x)\pi(\theta\,|\,\theta\in H_{1})\,dP_{H_{1}}(\theta)\\[6pt] =&\prod_{i=1}^{2}\left[{{n_{i}} \choose{x_{i}}} \frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})} \frac{\Gamma(a_{i}+x_{i})\Gamma(n_{i}+b_{i}-x_{i})}{\Gamma(n_{i}+b_{i}+a_{i})}\right]. \end{aligned} \end{equation}\]Portanto, o fator de Bayes \(Bf(\pmb{x})\) a favor de \(H_{0}\) é dado por:
\[\begin{equation} Bf(x)=\frac{\Gamma(C)\Gamma(D)\Gamma\left(\sum_{i=1}^{2}(a_{i}+b_{i})-2\right)}{\Gamma(C+D)\Gamma\left(\sum_{i=1}^{2}a_{i}-1\right)\Gamma\left(\sum_{i=1}^{2}b_{i}-1\right)\prod_{i=1}^{2} G_{i}}, \end{equation}\]em que, \(\textstyle G_{i}=\frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})}\frac{\Gamma(a_{i}+x_{i})\Gamma(n_{i}+b_{i}-x_{i})}{\Gamma(n_{i}+b_{i}+a_{i})}\) para \(i=1,2\).
Níveis de significância adaptativos
Finalmente, o nível de significância adaptativo descrito em [1] é dado por:
\[\begin{equation} \begin{aligned} \alpha_{\scriptscriptstyle \delta^{*}}&=\mathbb{P}(Bf(X) \leq 1\,|\, X \sim f_{\scriptscriptstyle H_{0}})\\ &=\displaystyle \sum\limits_{\substack{Bf(x) \leq 1}}\displaystyle \int_{\Theta}L(\theta\,|\,x )\pi(\theta\,|\,\theta\in H_{0})dP_{\scriptscriptstyle H_{0}}(\theta)=\sum\limits_{\substack{Bf(x) \leq 1}}f_{\scriptscriptstyle H_{0}}(\pmb{x}), \end{aligned} \end{equation}\] e o valor-P Bayesiano é definido como: \[\begin{equation} P-value(x_{0})=\sum\limits_{\substack{Bf(x)\leq Bf(x_{0})}} f_{H_{0}}(x). \end{equation}\]Assim, de maneira análoga ao t-test e z-test, a hipótese de igualdade entre as taxas de conversão \((H_{0})\) será rejeitada se:
\[ P-value(x_{0}) < \alpha_{\scriptscriptstyle \delta^{*}}. \]A vantagem de usar níveis adaptativos de significância é que eles estão em função do tamanho da amostra, de modo que eles não dependem do momento em que o experimento é interrompido, consequentemente, o p-hacking é evitado. Para elucidar a teoria até aqui apresentada faremos uma aplicação em um conjunto de dados de e-commerce.
Exemplo
Para nosso exemplo utilizamos um conjunto de dados disponibilizado pela datacamp sobre um site em que a palavra ‘tools’ foi alterada para ‘tips’ e o objetivo é avaliar a proporção de cliques no artigo, likes e shareds numa postagem. Os dados têm a seguinte estrutura:
| visit_date | condition | time_spent_homepage_sec | clicked_article | clicked_like | clicked_share |
|---|---|---|---|---|---|
| 2018-04-01 | tips | 49.01161 | 1 | 0 | 1 |
| 2018-04-01 | tips | 48.86452 | 1 | 0 | 0 |
| 2018-04-01 | tips | 49.07467 | 1 | 0 | 0 |
| 2018-04-01 | tips | 49.26011 | 0 | 1 | 0 |
| 2018-04-01 | tips | 50.37190 | 0 | 1 | 0 |
| 2018-04-01 | tips | 49.08458 | 1 | 0 | 0 |
em que os resultados obtidos no experimento são apresentados na tabela a seguir:
| Não | Sim | Não | Sim | Não | Sim | |
|---|---|---|---|---|---|---|
| tips | 422 | 88 | 196 | 314 | 497 | 13 |
| tools | 488 | 35 | 194 | 329 | 509 | 14 |
para os quais calculamos o fator de Bayes, o nível de significância adaptativo (Alpha) e o valor_P Bayesiano:
| Bf | Alpha | valor_P | |
|---|---|---|---|
| Like | 0.0000163 | 0.014841 | 0.0000001 |
| Article | 12.0126583 | 0.014841 | 0.3797618 |
| Shared | 39.6190247 | 0.014841 | 0.8324829 |
Observe que as conclusões aqui são feitas de maneira semelhante à abordagem frequentista, ou seja, a hipótese de igualdade será rejeitada quando o valor_P for menor que Alpha. No nosso exemplo, vemos que a alteração da palavra tips foi significativa para clicks em Like, ou seja, a troca do termo tools por tips gerou uma mudança nos Likes. Já os clicks em Article e Shared apresentaram um valor_P maior que Alpha, logo, não há evidências para afirmar que a troca do termo gere mudanças nos clicks em Article e Shared.
Referências
[1] Pereira C, Nakano E, Fossaluza V, Esteves L, Gannon M y Polpo A., 2017., Hypothesis tests for bernoulli experiments: Ordering the sample space by bayes factors and using adaptive significance levels for decisions. Entropy, 19:696.
[2] Flórez A y Correa J., 2015., Una propuesta metodológica para elicitar el vector de parámetros \(\pi\) de la distribución Multinomial., Comunicaciones en Estadística, 8(1):81–97.
[3] Bakshy E, Eckles D y Bernstein M., 2014., Designing and deploying online field experiments., 23rd ACM conference on the World Wide Web.
[4] Tang D, Agarwal A, O’Brien D y Meyer M., 2010, Overlapping experiment infrastructure: More, better, faster experimentation., 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining., 17–26.
[5] Kohavi R, Deng A, Frasca B, Walker T, Xu Y y Pohlmann N., 2013., Online controlled experiments at large scale., 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
[6] Trafimow D y Marks M., 2015., Editorial., Basic and Applied Social Psychology, 37:1–2.
[7] Wasserstein R y Lazar N., 2016., The asa statement on pvalues: Context, process, and purpose. The American Statistician, 70(2):129–133.