Test A/B pueden ser vistos como experimentos controlados que apoyan la toma de decisiones basadas en datos. Este tipo de experimentos son generalmente usados para medir el impacto de cambios realizados y comparar diferentes alternativas en campañas de marketing, productos de software o sitios web. En la actualidad, reconocidas empresas de tecnología emplean test A/B para apoyar la toma de decisiones, por ejemplo, Facebook [3], Google [4] y Microsoft [5].
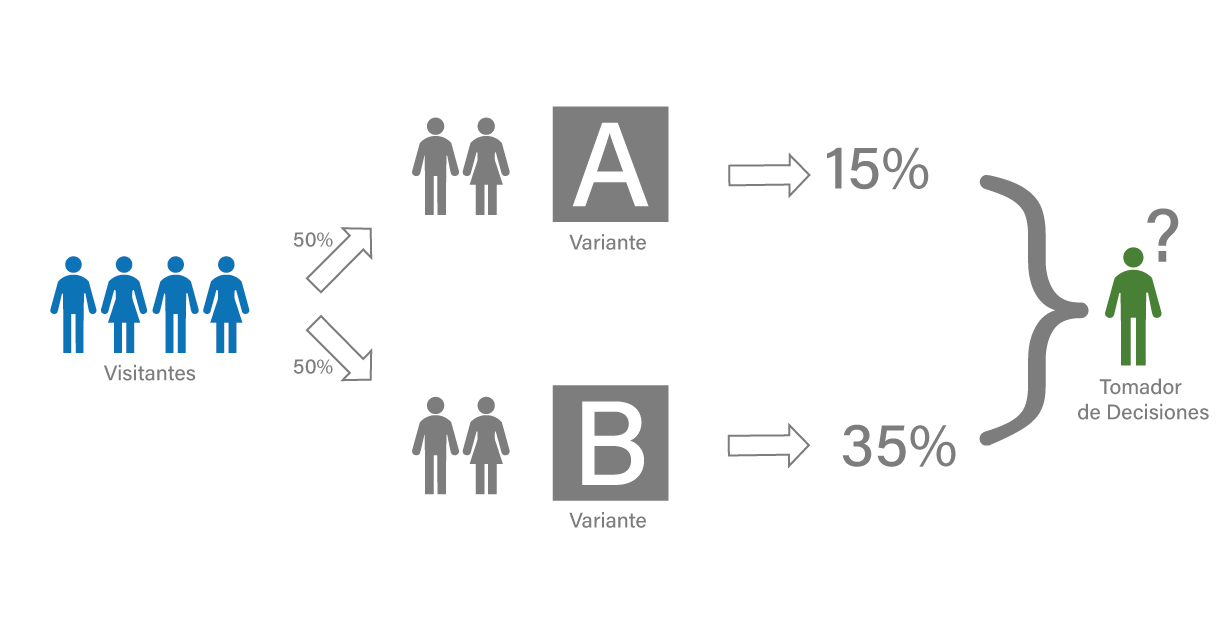
Como se muestra en la figura anterior, la idea de un test A/B es comparar las proporciones de éxito de cada variante realizada (en la imagen, Variante A y B). Para comparar esas proporciones, generalmente se usan los bien conocidos t-test y z-test, que resumen el resultado de la prueba a un valor-p, rechazando la hipótesis de igualdad entre las proporciones cuando el valor-p es menor que un nivel de significancia prefijado, generalmente 5%. Sin embargo, este tipo de metodologías basadas en valor-p (o test de significancia) han sido ampliamente criticadas desde diferentes puntos de vista [6][7]. Una de las criticas más frecuentes es conocida como p-hacking, en donde el experimento es detenido justo en el momento que el valor-p es menor que el nivel de significancia prefijado, favoreciendo así unas de las variantes.
Por otro lado, las metodologías Bayesianas están ganando cada vez más aceptación debido a su fácil interpretación e implementación. Aunque reciben algunas críticas por su sensibilidad en la selección de la distribución a priori, actualmente hay diversas formas de obtener distribuciones a priori apropiadas para cada situación, como es discutido en [2]. En esta publicación, presentamos la metodología desarrollada en [1] como una solución óptima para combatir el p-hacking y las diversas críticas interpretativas heredadas cuando se utiliza el valor-p como medida de decisión.
Supongamos que queremos entender si es necesario que una compañía implemente un nuevo sitio web o simplemente mantenga uno ya existente. Para eso, dividimos el numero de visitantes en dos grupos A y B, El grupo A representa los usuarios que visualizan el nuevo sitio web y el grupo B los usuarios que visitan el existente. Para comparar los dos sitios vamos a usar la proporción de conversiones en cada grupo, esto es, el número de visitantes que concluyen el objetivo deseado. Entonces, permita que \(X_{A}\) represente el número de conversiones en el grupo A y \(X_{B}\) represente el número de conversiones del grupo B. Note que \(X_{A}\) y \(X_{B}\) siguen una distribución Binomial, i.e, \(X_{A}\sim Bin(n_{A},\theta_{A})\) y \(X_{B}\sim Bin(n_{B},\theta_{B})\). Dónde \(n_{(.)}\) representa el número de usuarios en cada grupo y \(\theta_{(.)}\) representa la probabilidad de conversión en el respectivo grupo.
Modelo estadístico
Para probar si la proporción de conversiones son estadísticamente iguales, definimos las siguientes hipótesis:
\[\begin{equation}\label{Homogeneity_Bin} \begin{aligned} H_{0}:&\, \theta_{A}=\theta_{B}\\ H_{1}:&\, \theta_{A} \neq \theta_{B}. \end{aligned} \end{equation}\]Desde la perspectiva Bayesiana, la hipótesis se prueba utilizando el factor Bayes, que es definido como:
\[ Bf(x)=\frac{f_{H_{0}(x)}}{f_{H_{1}(x)}}=\frac{\displaystyle \int_{\Theta} L(\pmb{\theta}\,|\,\pmb{x})\pi(\theta\,|\,\theta\in H_{0})\,dP_{H_{0}}(\theta)}{\displaystyle \int_{\Theta} L(\pmb{\theta}\,|\,\pmb{x})\pi(\theta\,|\,\theta\in H_{1})\,dP_{H_{1}}(\theta)}. \]Con el fin de facilitar la notación, vamos a denotar los visitantes del grupo A como la población 1 y los del grupo B como la población 2. Así, tenemos que \(L(\pmb{\theta}\,|\,\pmb{x})\) es conocido como función de verosimilitud y que para nuestro caso es descrita por:
\[\begin{equation}\label{def:LikelihoodHonogenityBinomial} L(\pmb{\theta} \,|\, \pmb{x}) =\prod_{i=1}^{2} {{n_{i}}\choose{x_{i}}}\theta_{i}^{x_{i}}(1-\theta_{i})^{n_{i}-x_{i}} I(\theta_{i}\in (0,1)). \end{equation}\]También en el paradigma Bayesiano se asume que \(\theta_{A}\) y \(\theta_{B}\) tienen distribución de probabilidad, que en este caso es una distribución Beta para cada parámetro, esto es:
\[\begin{equation} \pi(\theta_{i})=\frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})}\theta_{i}^{a_{i}-1}(1-\theta_{i})^{b_{i}-1}I(\theta_{i}\in (0,1)),\qquad i=1,2. \end{equation}\]Con estas definiciones podemos computar la distribución predictiva sobre la hipótesis nula como:
\[\begin{equation} \begin{aligned} f_{\scriptscriptstyle H_{0}}(\pmb{x})=&\displaystyle \int_{\Theta} L(\pmb{\theta}\,|\,\pmb{x})\pi(\theta\,|\,\theta\in H_{0})\,dP_{H_{0}}(\theta)\\[6pt] =&\frac{\prod_{i=1}^{2}{{n_{i}}\choose{x_{i}}}\Gamma(D)\Gamma(C)\Gamma\left(\sum_{i=1}^{2}(a_{i}+b_{i})-2\right)}{\Gamma(D+C)\Gamma\left(\sum_{i=1}^{2}a_{i}-1\right)\Gamma\left(\sum_{i=1}^{2}b_{i}-1\right)}, \end{aligned} \end{equation}\]donde \(\textstyle D=\sum_{i=1}^{2}(a_{i}+x_{i})-1\), \(C=\sum_{i=1}^{2}(n_{i}+b_{i}-x_{i})-1\). Análogamente, la distribución predictiva sobre la hipótesis alternativa es dada por:
\[\begin{equation} \begin{aligned} f_{\scriptscriptstyle H_{1}}(\pmb{x})=&\displaystyle \int_{\Theta} L(\pmb{\theta}\,|\,\pmb{x})\pi(\theta\,|\,\theta\in H_{1})\,dP_{H_{1}}(\theta)\\[6pt] =&\prod_{i=1}^{2}\left[{{n_{i}} \choose{x_{i}}} \frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})} \frac{\Gamma(a_{i}+x_{i})\Gamma(n_{i}+b_{i}-x_{i})}{\Gamma(n_{i}+b_{i}+a_{i})}\right]. \end{aligned} \end{equation}\]Entonces, el factor de Bayes \(Bf(\pmb{x})\) en favor de \(H_{0}\) es dado por:
\[\begin{equation} Bf(x)=\frac{\Gamma(C)\Gamma(D)\Gamma\left(\sum_{i=1}^{2}(a_{i}+b_{i})-2\right)}{\Gamma(C+D)\Gamma\left(\sum_{i=1}^{2}a_{i}-1\right)\Gamma\left(\sum_{i=1}^{2}b_{i}-1\right)\prod_{i=1}^{2} G_{i}}, \end{equation}\]donde, \(\textstyle G_{i}=\frac{\Gamma(a_{i}+b_{i})}{\Gamma(a_{i})\Gamma(b_{i})}\frac{\Gamma(a_{i}+x_{i})\Gamma(n_{i}+b_{i}-x_{i})}{\Gamma(n_{i}+b_{i}+a_{i})}\) para \(i=1,2\).
Niveles de significancia adaptativos
Finalmente, el nivel de significancia adaptativo descrito en [1] es dado por:
\[\begin{equation} \begin{aligned} \alpha_{\scriptscriptstyle \delta^{*}}&=\mathbb{P}(Bf(X) \leq 1\,|\, X \sim f_{\scriptscriptstyle H_{0}})\\ &=\displaystyle \sum\limits_{\substack{Bf(x) \leq 1}}\displaystyle \int_{\Theta}L(\theta\,|\,x )\pi(\theta\,|\,\theta\in H_{0})dP_{\scriptscriptstyle H_{0}}(\theta)=\sum\limits_{\substack{Bf(x) \leq 1}}f_{\scriptscriptstyle H_{0}}(\pmb{x}). \end{aligned} \end{equation}\]y el valor-P Bayesiano es difinido como:
\[\begin{equation} P-value(x_{0})=\sum\limits_{\substack{Bf(x)\leq Bf(x_{0})}} f_{H_{0}}(\pmb{x}) \end{equation}\]Así, de forma análoga que en t-test y z-test, la hipótesis de igualdad entre las proporciones de conversión \((H_{0})\) será rechazada si:
\[ P-value(x_{0}) < \alpha_{\scriptscriptstyle \delta^{*}}. \]La ventaja de usar niveles de significancia adaptativos es que ellos están en función del tamaño de muestra, por tanto, no dependen del momento en el que el experimento es detenido, consecuentemente el p-hacking es evitado. Para dilucidar la teoría presentada hasta aquí, haremos una aplicación en un conjunto de datos de e-commerce.
Ejemplo
A continuación presentamos un ejemplo utilizando un set datos disponible en datacamp sobre un sitio web donde se cambió la palabra ‘tools’ por ‘tips’ y se pretende evaluar la proporción de clicks en el articulo, likes y Shareds en un post. Los datos presentan la siguiente estructura:
| visit_date | condition | time_spent_homepage_sec | clicked_article | clicked_like | clicked_share |
|---|---|---|---|---|---|
| 2018-04-01 | tips | 49.01161 | 1 | 0 | 1 |
| 2018-04-01 | tips | 48.86452 | 1 | 0 | 0 |
| 2018-04-01 | tips | 49.07467 | 1 | 0 | 0 |
| 2018-04-01 | tips | 49.26011 | 0 | 1 | 0 |
| 2018-04-01 | tips | 50.37190 | 0 | 1 | 0 |
| 2018-04-01 | tips | 49.08458 | 1 | 0 | 0 |
donde los resultados obtenidos en el experimento son presentados en la siguiente tabla:
| No | Si | No | Si | No | Si | |
|---|---|---|---|---|---|---|
| tips | 422 | 88 | 196 | 314 | 497 | 13 |
| tools | 488 | 35 | 194 | 329 | 509 | 14 |
para los cuales calculamos el factor de Bayes, el nivel de significancia adaptativo (Alpha) y el valor_P Bayesiano:
| Bf | Alpha | valor_P | |
|---|---|---|---|
| Like | 0.0000163 | 0.014841 | 0.0000001 |
| Article | 12.0126583 | 0.014841 | 0.3797618 |
| Shared | 39.6190247 | 0.014841 | 0.8324829 |
Note que las conclusiones aquí se hacen de forma similar que en abordaje frecuentista, es decir, la hipótesis de igualdad será rechazada cuando el valor_P es menor que Alpha. Para nuestro ejemplo vemos que cambiar la palabra ‘tips’ fue significativa para clicks en Like, esto significa que cambiar la palabra tools por tips generó diferencia de los clicks en Likes. Ahora, clicks en Article y Shared tuvieron un valor_P mayor a ‘Alpha’, por tanto, no hay evidencia para afirmar que cambiar la palabra genere diferencia de los clicks en Article y Shared.
Referencias
[1] Pereira C, Nakano E, Fossaluza V, Esteves L, Gannon M y Polpo A., 2017., Hypothesis tests for bernoulli experiments: Ordering the sample space by bayes factors and using adaptive significance levels for decisions. Entropy, 19:696.
[2] Flórez A y Correa J., 2015., Una propuesta metodológica para elicitar el vector de parámetros \(\pi\) de la distribución Multinomial., Comunicaciones en Estadística, 8(1):81–97.
[3] Bakshy E, Eckles D y Bernstein M., 2014., Designing and deploying online field experiments., 23rd ACM conference on the World Wide Web.
[4] Tang D, Agarwal A, O’Brien D y Meyer M., 2010, Overlapping experiment infrastructure: More, better, faster experimentation., 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining., 17–26.
[5] Kohavi R, Deng A, Frasca B, Walker T, Xu Y y Pohlmann N., 2013., Online controlled experiments at large scale., 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
[6] Trafimow D y Marks M., 2015., Editorial., Basic and Applied Social Psychology, 37:1–2.
[7] Wasserstein R y Lazar N., 2016., The asa statement on pvalues: Context, process, and purpose. The American Statistician, 70(2):129–133.